题目描述
小蓝在 LQ 集市上发现一个套手镯的游戏,在一个大小为 $10^8 \times 10^8$ 矩形平面上摆放着 $N$ 个圆形的手镯。玩家可以将一个大小为 $w \times h$ 的矩形方框放置在这个平面上(玩家只可以沿着水平/垂直方向放置方框,即可以将方框旋转 $90$ 度,但不可以旋转至其他角度),位于这个矩形方框内部的手镯就是玩家获得的奖励。
可以将这个矩形平面看作是一个二维坐标系,左下角的坐标为 $(0, 0)$。手镯和方框的厚度可以忽略不计, 允许多个手镯重叠放置。
小蓝想要尝试一次,请问他最多可以获得多少手镯?
输入格式
第一行输入三个整数 $N, w, h$。
接下来输入 $N$ 行,每行三个整数 $x, y, r$,表示第 $i$ 个手镯的圆心坐标和半径。
提示
#### 【样例说明】
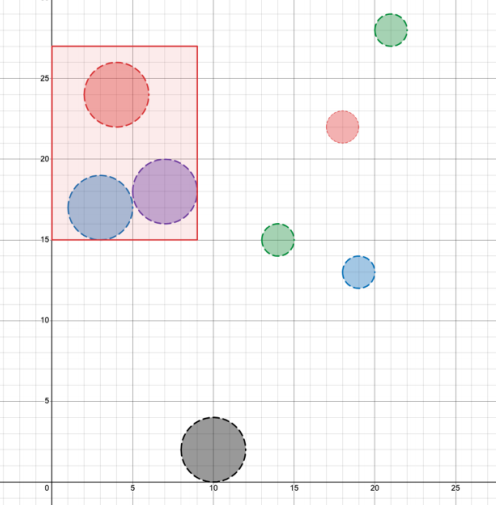
上图展示了一种可能的答案。
#### 【评测用例规模与约定】
对于 $50\%$ 的评测用例:$1 \le N \le 100$,$1 \le w, h, x, y, r \le 200$。
对于 $100\%$ 的评测用例:$1 \le N \le 1000$,$1 \le w, h, x, y, r \le 10^8$,$1 \le \min\{w, h\} \le 200$。保证所有手镯都位于平面内部。