题目描述

众所周知,由 $n-1$ 条边连接 $n$ 个点所形成的单连通块被称作树。
假如取树上的某个结点定作树根,结点 $x$ 到树根的距离为 $d_x$,那么定义结点 $u$ 的父结点也就是在所有与 $u$ **直接相连**的结点中,与树根的距离为 $d_u-1$ 的结点。特殊的,根结点没有父结点。
现在你拿到了一棵树,但与普通的树不同的是,这棵树的树根是实时变化的。
试问,假如结点 $u$ 为树根,那么结点 $v$ 的父结点编号是什么?
输入格式
第一行包含一个整数 $n$ $(2 \le n \le 10^5)$,表示树的结点数。
第二行包含 $n-1$ 个数,第 $i$ 个数 $d_i$ $(1 \le d_i \le i)$ 表示结点 $i+1$ 与结点 $d_i$ 间存在一条边。
第三行包含一个整数 $q$ $(1\le q\le 2\times 10^5)$,表示询问个数。
其后 $q$ 行,每行包含两个整数 $u,v$ $(1 \le u,v \le n)$,表示询问。
易得在给定的约束条件下,图一定是连通的。
输出格式
对于每次询问,在一行内输出一个整数,表示树根为 $u$ 时结点 $v$ 的父结点编号。如果不存在父结点,输出 `-1`。
样例输入 #1
5
1 1 2 2
5
1 4
1 2
2 3
4 5
5 2
提示
对于样例:
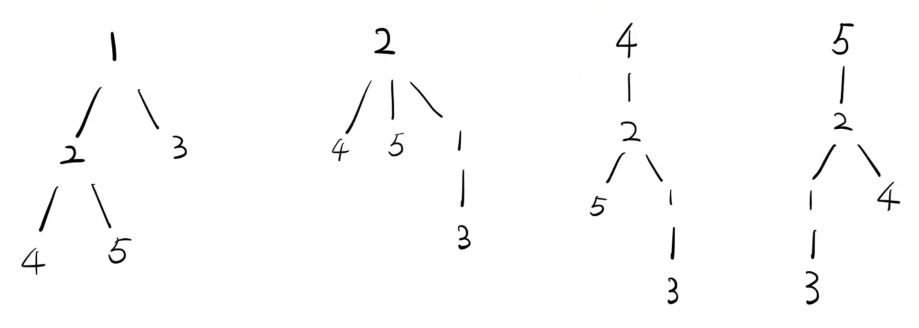
来源
2023-04-16 ZJNU 天梯赛模拟场 L3-1