***本题与“その1”以及“その2”的询问以及数据范围均不同，请仔细读题。*** --- With the development of the Internet, the industrial structure of Cosmic-Village has undergone great changes, and now it has become the logistics center of the entire universe! The logistics center has a group of packing robots that are responsible for packing items into boxes, but the size of each item and each box are fixed. There is a batch of items $a_1,a_2,\cdots,a_n$ and a batch of boxes $b_1,b_2,\cdots,b_m$. The $i$-th item has size $length(a_i)\times width(a_i)$, and the $j$-th box has size $length(b_j)\times width(b_j)$. We say that item $a_i$ can ***non-rotationally fits*** into box $b_j$ if and only if the following condition hold: - $length(a_i)\le length(b_j),\ width(a_i)\le width(b_j)$ Obviously, these robots are not very smart. So Cosmic-Cat, Cosmic-Village's technical advisor, decided to upgrade some of the robots' systems. Now, these upgraded robots learn to rotate items! We say that item $a_i$ can ***rotationally fits*** into box $b_j$ if at least one of the following conditions hold: - $length(a_i)\le length(b_j),\ width(a_i)\le width(b_j)$ - $length(a_i)\le width(b_j),\ width(a_i)\le length(b_j)$ The ***total rotation fit*** is the total number of item-box pairs $(a_i,b_j)$ such that $a_i$ can ***rotationally fits*** into $b_j$, and similarly, the ***total non-rotation fit*** is the total number of item-box pairs $(a_i,b_j)$ such that $a_i$ can ***non-rotationally fits*** into $b_j$.  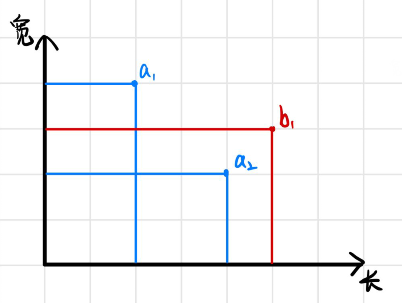Figure: Only $a_2$ can ***non-rotationally fits*** into box $b_1$ so the ***total non-rotational fit*** is $1$; Both $a_1$ and $a_2$ can ***rotationally fits*** into box $b_1$ so the ***total rotational fit*** is $2$. For this task, you're given the size of $n$ items and $m$ boxes, as instance $I$. You need to construct another instance $J$ with any number of items and any number of boxes, and ensure that the ***total rotational fit*** of instance $I$ is exactly equal to the ***total non-rotational fit*** of your instance $J$. --- 随着扈櫣魍的发展，星际村的产业结构发生了大变化，现在它成为了全宇宙的物流中心！物流中心有一批打包机器人，专门负责将物品打包进箱子里，但每个物品的尺寸和箱子的尺寸都是固定的。 现在有一批物品 $a_1,a_2,\cdots,a_n$ 等待被打包，第 $i$ 个物品的长度为 $length(a_i)$，宽度为 $width(a_i)$；还有一堆箱子 $b_1,b_2,\cdots,b_m$ 可以用来打包，第 $j$ 个箱子的长度为 $length(b_j)$，宽度为 $width(b_j)$。 这批打包机器人有点笨，假设现在等待打包的物品长宽为 $length(a),width(a)$，箱子长宽为 $length(b),width(b)$，那么只有当下列条件满足时，机器人才能将物品打包进这个箱子里： $$ length(a)\le length(b),\ width(a)\le width(b) $$ 于是技术顾问星际猫对某些打包机器人进行了一次升级，现在它们学会了旋转物品！换言之，他们可以通过将物品旋转 $90^{\circ}$ 及其倍数后，再尝试将物品打包进箱子中，即满足下列两种情况的任意一种即可： $$ length(a)\le length(b),\ width(a)\le width(b)\\ length(a)\le width(b),\ width(a)\le length(b) $$ 我们定义“总旋转适配值”表示有多少对“物品-盒子”数对 $(a_i,b_j)$ 满足物品 $a_i$ 可以在旋转（或者不旋转）后打包进盒子 $b_j$ 中。  如上图，物品 $a_2$ 无需旋转就可以放进盒子 $b_1$ 中，而物品 $a_1$ 需要通过旋转 $90^{\circ}$ 来放进盒子 $b_1$ 中。因此存在两对数对 $(a_1,b_1)$ 和 $(a_2,b_1)$，于是该图中的“总旋转适配值”为 $2$。 同时，生产线上还有一批没有被升级的打包机器人，他们无法对物品进行旋转。于是我们再定义“总不旋转适配值”表示有多少对“物品-盒子”数对 $(a_i,b_j)$ 满足物品 $a_i$ 不通过旋转后可以直接打包进盒子 $b_j$ 中。对于上图，明显“总不旋转适配值”为 $1$。 在这道题目中，给定 $n$ 个物品的长宽以及 $m$ 个盒子的长宽，作为方案 $I$。你需要构造出另一种方案 $J$，其中包含任意个物品以及任意个盒子，并使得方案 $J$ 的“总不旋转合适值”与题目给定方案 $I$ 的“总旋转合适值”相同。限制详见输出部分。

The first line contains a single integer $n$ --- the amount of items. Next $n$ lines, each line contains two integers $length(a_i)$ and $width(a_i)$, representing the $i$-th item's size. Next line contains a single integer $m$ --- the amount of boxes. Next $m$ lines, each line contains two integers $length(b_j)$ and $width(b_j)$, representing the $j$-th box's size. <font color='red'>$1\le n,m\le 500,000$</font> <font color="red">$1\le length(a_i),length(b_i),width(a_i),width(b_i)\le 500,000$</font> --- 第一行包含一个正整数 $n$。 其后 $n$ 行，第 $i$ 行包含两个正整数 $w(a_i),h(a_i)$，分别表示每个物品的长宽。 第 $n+2$ 行包含一个正整数 $m$。 其后 $m$ 行，第 $j$ 行包含两个正整数 $w(b_j),h(b_j)$，分别表示每个盒子的长宽。 <font color="red">$1\le n,m\le 500000$</font> <font color="red">$1\le length(a_i),length(b_i),width(a_i),width(b_i)\le 500,000$</font>

Your output instance $J$ should also follow the sample format as the input instance $I$: The first line contains a single integer $n'$ --- the amount of items in your constructed instance. Next $n$ lines, each line contains two integers $length'(a_i)$ and $width'(a_i)$, representing the $i$-th item's size. Next line contains a single integer $m'$ --- the amount of boxes in your constructed instance. Next $m$ lines, each line contains two integers $length'(b_j)$ and $width'(b_j)$, representing the $j$-th box's size. **Range Limit:** $1\le n',m'\le 720,000$ $1\le length'(a_i),length'(b_i),width'(a_i),width'(b_i)\lt 1,000,000$ If there are multiple solutions, print any of them. It is guaranteed that at least one solution exists within the given range. --- 第一行输出一个正整数 $n'$，表示你的方案中物品的数量。 其后 $n'$ 行，第 $i$ 行输出两个正整数 $length'(a_i),width'(a_i)$，分别表示每个物品的长宽，以空格隔开。 第 $n'+2$ 行输出一个正整数 $m'$，表示你的方案中盒子的数量。 其后 $m'$ 行，第 $j$ 行包含两个正整数 $length'(b_j),width'(b_j)$，分别表示每个盒子的长宽，以空格隔开。 你只需要输出任意一种合法的方案即可。 **限制：** $1\le n',m'\le 720,000$ $1\le length'(a_i),length'(b_i),width'(a_i),width'(b_i)\lt 1,000,000$ 数据保证一定存在至少一种满足上述条件的合法构造方案。

Idea from ECNU, prepared by StelaYuri | For 220515 Final 2