动态规划(Dynamic Programming)的实现形式之一是递推，因此递推在OI中十分重要。在某信息学的分支学科中，LC学会了如何求一阶线性递推数列。由于他现在正在学习主干学科，因此希望知道求出N阶线性递推数列。为此，他了解到了以下内容：
一个N阶线性递推式是这样的式子：

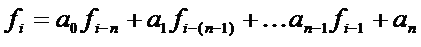
也就是说，这个数列的每一项都是由它之前连续N项加权相加所得。其中还包括一个常数an。
例如，当N=2，a0=al=1，a2=O时，这个式子就是我们熟悉的斐波那契数列。当然，作为边界条件，f0,f1,…fn-1都是已知的。
LC对这如何去求这个式子一筹莫展，因此请你来帮助他。你的任务就是对于一个给定的N阶线性递推式，求出它的第K项是多少。
【数据规模】
对于50％的数据：N≤K≤10^6
对于lOO%的数据：
1 N≤K≤101^8
1≤ai,fi≤10^4

第一行两个整数：N、K，其中N表示这个式子是N阶线性递推式，K表示你需要求的那一项。
第二行有N+1个整数：a0，a1…an，表示这个递推式的系数。
第三行有N个整数：f0,f1,…fn-1表示数列的初始值。

只有一行，其中只有一个整数，表示这个数列第K项的值。由于数据较大，你只需输出结果mod 9973的值。