今年8月，P教授要去北京看奥运，但是它割舍不下自己的一大堆智力玩具。于是，他决定把所有的玩具都装箱运到北京去，这样便可在看比赛的同时摆弄智力玩具。
P教授使用自己的物体维数压缩器ODZ (Object Dimension Zipper) 来给玩具装箱。ODZ可以将任意物品变成一维，再装到一种特殊的一维容器中。P教授有n件玩具，编号为1到n，第i件玩具经过ODZ处理后的长度是ci，为了方便整理，P教授要求在一个一维容器中的玩具编号是连续的。同时，如果一个一维容器中有多个玩具，那么相邻两件玩具之间应该加入1个单位的填充物。形式地说，如果将第i件到第j件玩具放在一个容器中(I < j)，那么容器的长度将为：

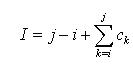
制作容器的费用与容器的长度有关。根据P教授的研究，如果容器长度为I，那么其制作费用为(l-L)^2，其中L是一个经过复杂计算推导出的常量。P教授毫不关心容器的数目，并且可以制造出任意长度的容器（甚至超过L），但他希望你帮他求出最小的制作费用。

第一行包含玩具数目n和常量L，并用一个空格隔开。此后n行，每行一个整数ci，表示第i件玩具被处理后的一位长度。输入数据保证n <= 50000且1 <= L, ci <= 10⁷对所有i成立。

仅包含一个整数，表示最小的制作费用。