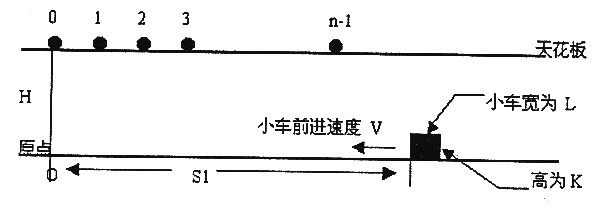
在高为 $H$ 的天花板上有 $n$ 个小球，体积不计，位置分别为 $0,1,2,\cdots,n-1$。在地面上有一个小车（长为 $L$，高为 $K$，距原点距离为 $S_1$）。已知小球下落距离计算公式为 $d＝\dfrac 1 2 gt^2$，其中 $g=10$，$t$ 为下落时间。地面上的小车以速度 $V$ 前进。  小车与所有小球同时开始运动，当**小球距小车的距离** $\le 0.00001$ 时，即认为小球被小车接受（小球落到地面后不能被接受）。 请你计算出小车能接受到多少个小球。

$H,S_1,V,L,K,n$ $(1 \le H,S_1,V,L,K,n \le 100000)$

小车能接受到的小球个数。

**把小车理解为没有挡板。**当球落入车的尾部时，算作落入车内。

NOIP2002提高