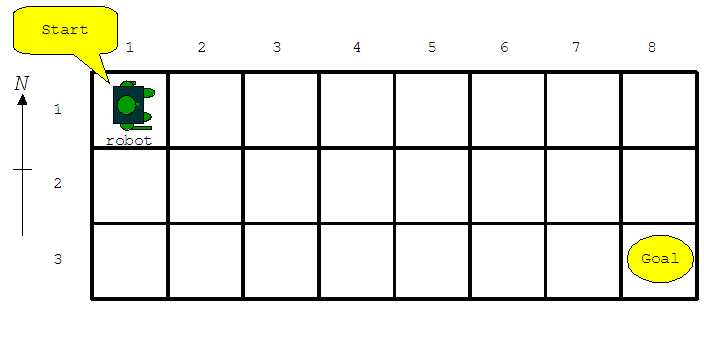
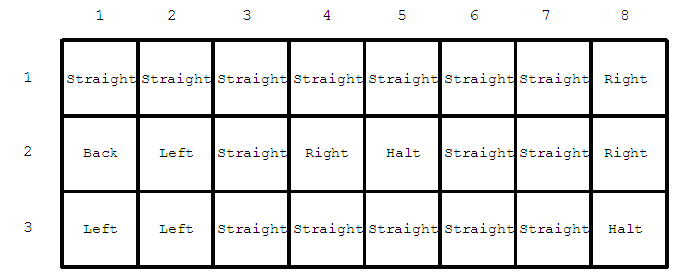
让我们来玩一个机器人游戏，游戏在一个长方形网格上进行，机器人最初被安放在长方形网格的左上角且面朝东，而游戏的目标就是使到达右下网格。  机器人可以执行以下 $5$ 种操作： - `Straight`: 保持机器人当前的方向，并前进一格。 - `Right`: 右转 $90$ 度，并前进一格。 - `Back`: 转 $180$ 度，并前进一格。 - `Left`: 左转 $90$ 度，并前进一格。 - `Halt`: 停在原地，并结束游戏。 每个方格上其中一种操作指令（如下图所示）。机器人会执行方格上的指令，除非你给了它其他的指令。每次你给机器人额外的指令，需要付出额外的代价。  机器人可以经过同一个方块多次。如果你在游戏过程中，让机器人走出边界或者在到达目标之前执行了 `Halt` 指令，你都将失败。 现在你的任务是计算最小的代价，使机器人从起点到达终点。

第一行包含两个整数 $w,h$ $(2 \le h \le 30, 2 \le w \le 30)$，表示列数和行数。 接下来 $h$ 行，每行包含 $w$ 个整数，第 $i$ 行第 $j$ 个整数 $s_{i,j}$ 表示该位置上的指令。每个位置上的整数代表的含义如下： - $0$: `Straight` - $1$: `Right` - $2$: `Back` - $3$: `Left` - $4$: `Halt` 最后一行包含 $4$ 个整数 $c_0, c_1, c_2, c_3$ $(1 \le c_i \le 9)$，分别表示使用 `Straight`, `Right`, `Back` 和 `Left` 命令的代价。 保证 `Halt` 命令将出现在目标位置，但也可能出现在其它方格中。

输出机器人从起点到终点的最小代价。