> $\tt\Huge\textbf{6}$ 我们定义 $f(n)$ 表示由 $n$ 个 $6$ 组成的非负整数。例如：$f(1) = 6, f(2) = 66, f(4) = 6666$。特殊的，$f(0) = 0$。 再定义 $g(n)$ 表示 $f(n)$ 的前缀和函数，即 $g(n) = \sum\limits_{i=0}^n f(i)$。例如：$g(2) = f(0) + f(1) + f(2) = 0 + 6 + 66 = 72$。 --- 现在有一棵由 $N$ 个点组成的树，每个结点分别编号为 $1, 2, 3, \dots, N$，令**编号为 $1$ 的结点**作为这棵树的根结点。 每个结点一开始都有一个权值，第 $i$ 个结点的初始权值为 $a_i$。 我们令 $S_p$ 表示**以编号为 $p$ 的结点作为根结点时**，这棵子树上所有结点所组成的集合。 有 $Q$ 次操作，每次操作描述为以下两种格式之一： - `1 p x`：表示修改。请对于所有 $i \in S_p$，更新 $a_i := a_i + x$（即对于所有位于 $p$ 的子树上的结点 $i$，将其权值加上 $x$）。 - `2 p`：表示询问。请计算 $\sum\limits_{i \in S_p} g(a_i)$ 的值（即对于所有位于 $p$ 的子树上的结点 $i$，计算 $g(a_i)$ 求和的结果）。如果你觉得这个询问有点困难，你也可以输出 $6^p$ 的个位来当作答案哦。 对于每次询问操作，请输出计算的结果。答案可能很大，输出对 $10^9 + 7$ 取模后的结果即可。

第一行包含一个整数 $N$，表示树上结点的数量。 第二行包含 $N$ 个整数 $a_1, a_2, \dots, a_n$，分别表示每个结点的初始权值。 接下来 $N - 1$ 行，每行包含两个整数 $u_i, v_i$，表示树上的一条边连接的两个结点。 接下来一行包含一个整数 $Q$，表示操作的次数。 接下来 $Q$ 行，每行表示一次操作，格式详见题面所述。 - $1 \le N, Q \le 2 \times 10^5$ - $0 \le a_i, x \le 10^9$ - $1 \le u_i, v_i, p \le n$ - $u_i \ne v_i$ - 保证给定的 $n-1$ 条边一定能够组成一张包含 $n$ 个结点的连通图

对于每次询问操作，请输出一个整数，表示计算的结果。相邻两个整数之间请用空格或换行等空白字符隔开。 答案可能很大，输出对 $10^9 + 7$ 取模后的结果即可。

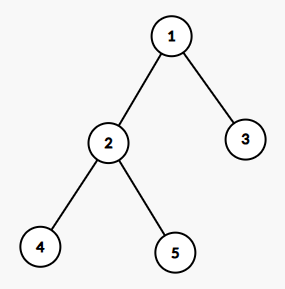
**【样例一解释】**  对于第一个询问，发现 $3$ 的子树只有 $3$ 这个点本身，答案为 $g(a_3) = g(3) = 738$。 对于第二个询问，发现 $2$ 的子树上点的集合 $S_2 = \{2, 4, 5\}$，则答案为 $g(a_2) + g(a_4) + g(a_5) = g(2) + g(4) + g(5) = 72 + 7404 + 74070 = 81546$。 对于第三个询问，发现 $1$ 的子树上点的集合 $S_1 = \{1, 2, 3, 4, 5\}$，则答案为 $g(a_1) + g(a_2) + g(a_3) + g(a_4) + g(a_5) = 82290$。 **【样例二解释】** 五次修改操作可以将各点的权值更新为与样例一的初值相同的结果。其它均与样例一相同。