题目描述
### 背景知识
#### 深度优先搜索与 DFS 序
深度优先搜索算法(DFS)是一种用于遍历或搜索树或图的算法。以下伪代码描述了在树 $T$ 上进行深度优先搜索的过程:
```text
procedure DFS(T, u, L) // T 是被深度优先搜索的树
// u 是当前搜索的节点
// L 是一个链表,保存了所有节点被第一次访问的顺序
append u to L // 将节点 u 添加到链表 L 的末尾
for v in u.children do // 枚举节点 u 的所有子节点 v
DFS(T, v) // 递归搜索节点 v
```
令 $r$ 为树 $T$ 的根,调用 `DFS(T, r, L)` 即可完成对 $T$ 的深度优先搜索,保存在链表 $L$ 中的排列被称为 DFS 序。相信聪明的你已经发现了,如果枚举子节点的顺序不同,最终得到的 DFS 序也会不同。
#### 逆序对
给定一个长度为 $n$ 的整数序列 $a_1,a_2,\cdots,a_n$,该序列的逆序对数量是同时满足以下条件的有序数对 $(i,j)$ 的数量:
- $1 \le i \lt j \le n$
- $a_i \gt a_j$
### 问题求解
给定一棵 $n$ 个节点的树,其中节点 $r$ 为根。求该树所有可能的 DFS 序中逆序对数量之和。
输入格式
第一行输入两个整数 $n,r$ $(2 \le n \le 3 \times 10^5,\ 1 \le r \le n)$ 表示树的大小与根节点。
对于接下来的 $(n−1)$ 行,第 $i$ 行输入两个整数 $u_i$ 与 $v_i$ $(1 \le u_i,v_i \le n)$,表示树上有一条边连接节点 $u_i$ 与 $v_i$。
输出格式
输出一行一个整数,表示该树所有可能的 DFS 序中逆序对数量之和。由于答案可能很大,请对 $10^9+7$ 取模后输出。
样例输入 #1
5 3
1 5
2 5
3 5
4 3
样例输入 #2
10 5
10 2
2 5
10 7
7 1
7 9
4 2
3 10
10 8
3 6
提示
下图展示了样例 1 中的树。
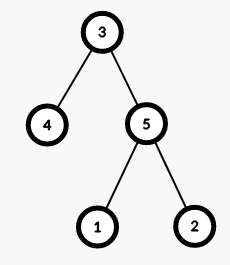
该树共有 $4$ 种可能的 DFS 序:
- $\{3,4,5,1,2\}$,有 $6$ 个逆序对;
- $\{3,4,5,2,1\}$,有 $7$ 个逆序对;
- $\{3,5,1,2,4\}$,有 $5$ 个逆序对;
- $\{3,5,2,1,4\}$,有 $6$ 个逆序对。
因此答案为 $6+7+5+6=24$。
来源
2022年中国高校计算机大赛-团体程序设计天梯赛(GPLT) L3-2