$\tt{Big Snail}$ 先生研究亚得里亚海海岸线时提出以下问题：给定长度为 $n$ 的地形高度序列 $h_1, h_2, \ldots, h_n$。对于 $q$ 个查询，每个查询要求计算在 **海平面上升 $x_i$ 米** 后，区间 $[l_i, r_i]$ 内的 **岛屿数量**。 **岛屿定义**：极大连续区间，满足该区间内所有地形高度 **严格大于** 当前海平面，且无法向两侧扩展。

第一行包含两个整数 $n$ 和 $q$（$1 \leq n, q \leq 2 \times 10^5$） 第二行包含 $n$ 个整数 $h_1, h_2, \ldots, h_n$（$0 \leq h_i \leq 10^9$） 接下来 $q$ 行每行包含三个整数 $l_i$, $r_i$, $x_i$（$1 \leq l_i \leq r_i \leq n$，$0 \leq x_i \leq 10^9$）

输出 $q$ 行，每行对应查询的岛屿数量

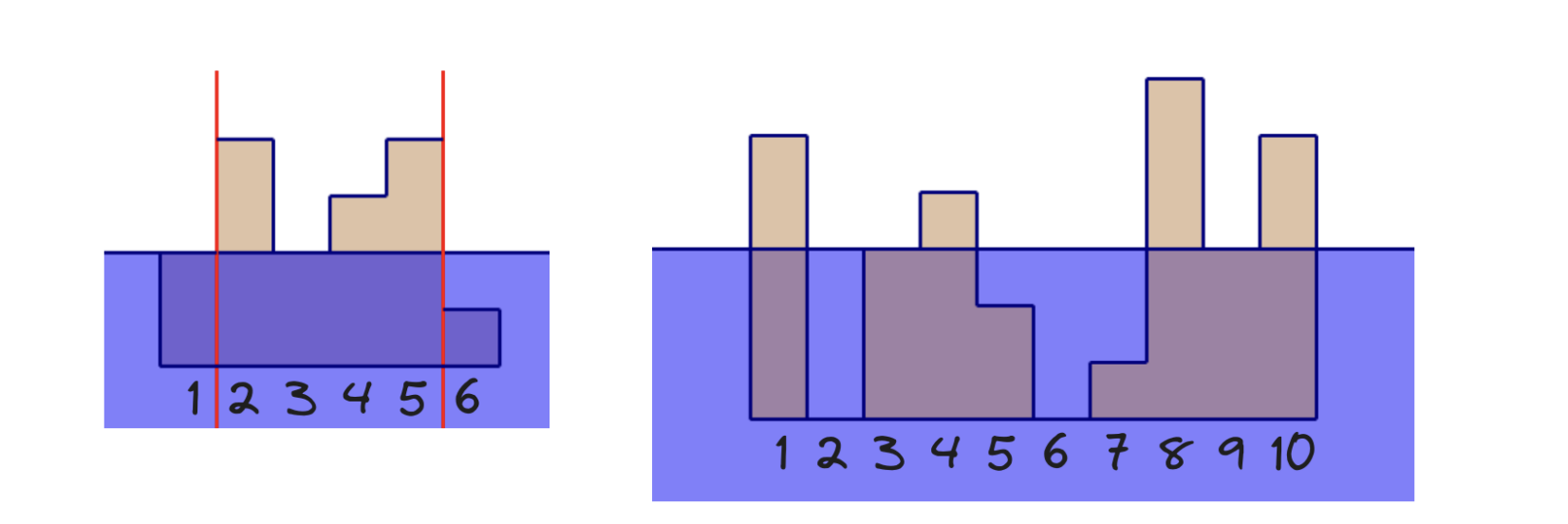
第一个样例解释： - 查询 $[2,5]$ 且 $x_i = 2$：岛屿区间为 $[2,2]$ 和 $[4,5]$ - 查询 $[3,5]$ 且 $x_i = 3$：岛屿区间为 $[5,5]$ - 查询 $[3,4]$ 且 $x_i = 4$：所有地形被淹没，岛屿数为 0 第二个样例解释： - 查询 $[3,9]$ 且 $x_i = 1$：岛屿区间为 $[3,5]$ 和 $[8,9]$ - 查询 $[1,10]$ 且 $x_i = 3$：岛屿区间为 $[1,1]$, $[4,4]$, $[8,8]$, $[10,10]$ - 查询 $[1,10]$ 且 $x_i = 2$：岛屿区间为 $[1,1]$, $[3,4]$, $[8,10]$