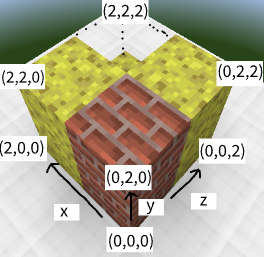
Farmer John 有一块立方体形状的奶酪，它位于三维坐标空间中，从 $(0,0,0)$ 延伸至 $(N,N,N)$（$2≤N≤1000$）。Farmer John 将对他的奶酪块执行一系列 $Q$（$1≤Q≤2⋅10^5$）次更新操作。 对于每次更新操作，FJ 将从整数坐标 $(x,y,z)$ 到 $(x+1,y+1,z+1)$ 处切割出一个 $1×1×1$ 的奶酪块，其中 $0≤x,y,z<N$。输入保证在 FJ 切割的位置上存在一个 $1×1×1$ 的奶酪块。由于 FJ 正在玩牛的世界，当下方的奶酪被切割后，重力不会导致上方的奶酪掉落。 在每次更新后，输出 FJ 可以将一个 $1×1×N$ 的砖块插入奶酪块中的方案数，使得砖块的任何部分都不与剩余的奶酪重叠。砖块的每个顶点在全部三个坐标轴上均必须具有整数坐标，范围为 $[0,N]$。FJ 可以随意旋转砖块。

输入的第一行包含 $N$ 和 $Q$。 以下 $Q$ 行包含 $x$，$y$ 和 $z$，为要切割的位置的坐标。

在每次更新操作后，输出一个整数，为所求的方案数。

### 样例解释 在前三次更新操作后，$[0,1]×[0,2]×[0,1]$ 范围的 $1×2×1$ 砖块与剩余的奶酪不重叠，因此它贡献了答案。