Farmer John 的 $N$ 头奶牛每头都有一种最喜欢的颜色。奶牛们的编号为 $1\ldots N$，每种颜色也可以用 $1\ldots N$ 中的一个整数表示。 存在 $M$ 对奶牛 $(a,b)$，奶牛 $b$ 仰慕奶牛 $a$。有可能 $a=b$，此时一头奶牛仰慕她自己。对于任意颜色 $c$，如果奶牛 $x$ 和 $y$ 都仰慕一头喜欢颜色 $c$ 的奶牛，那么 $x$ 和 $y$ 喜欢的颜色相同。 给定这些信息，求一种奶牛喜欢颜色的分配方案，使得每头奶牛最喜欢的颜色中不同颜色的数量最大。由于存在多种符合这一性质的分配方案，输出字典序最小的（这意味着你应当依次最小化分配给奶牛 $1 \ldots N$ 的颜色）。

输入的第一行包含 $N$ 和 $M$。 以下 $M$ 行每行包含两个空格分隔的整数 $a$ 和 $b$（$1\le a,b\le N$），表示奶牛 $b$ 仰慕奶牛 $a$。同一对奶牛可能会在输入中多次出现。

对于 $1\ldots N$ 中的每一个 $i$，用一行输出分配给奶牛 $i$ 的颜色。

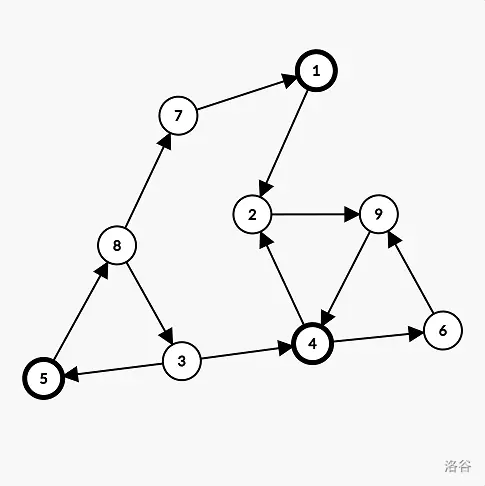
在下图中，用粗边框圆表示的是最喜欢颜色 $1$ 的奶牛。  对于 $100\%$ 的数据，$1\le N,M\le 2\times 10^5$。