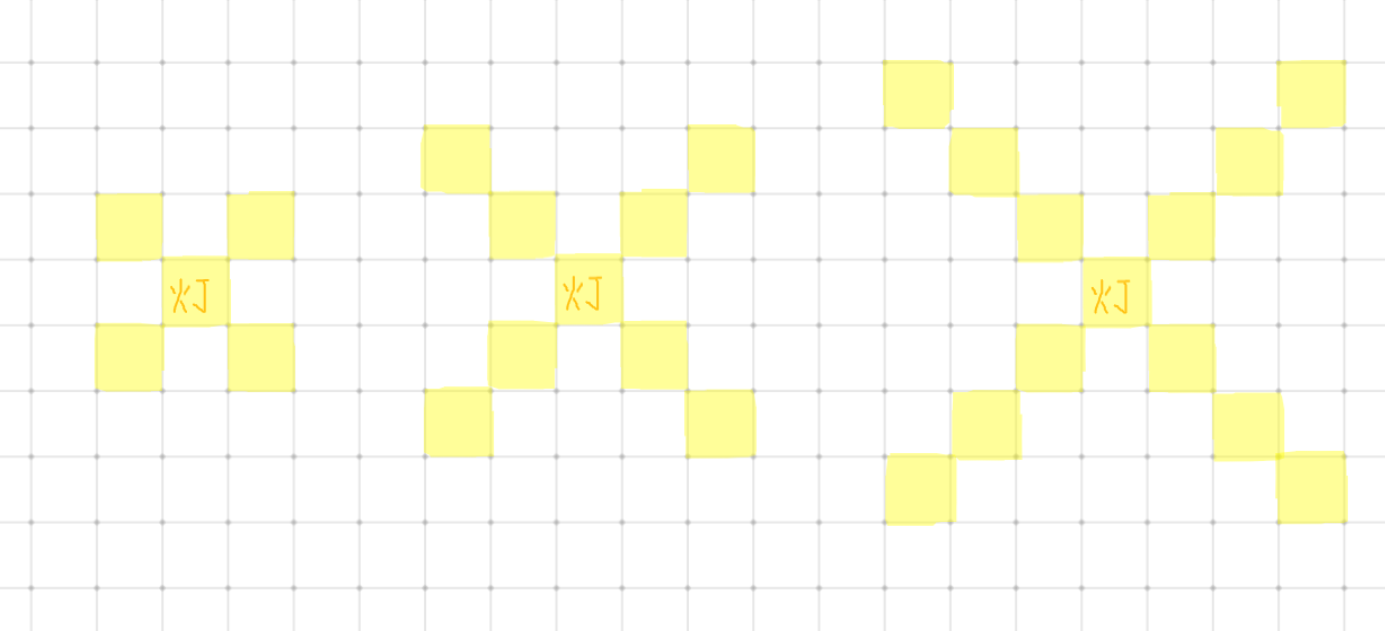
Alice 和 Bob 正在玩一个建造类型的游戏。 给定一个 $n\times m$ 的棋盘，Alice 和 Bob 可以在棋盘的格子上建造灯塔。再给定一个 $k$，表示每个灯塔的侦测范围。 灯塔的侦测范围是斜四向的，且随着 $k$ 增大而增大。 下方例子中，从左往右分别表示 $k=1,2,3$ 的时候，灯塔能侦测到的格子的范围：  Alice 和 Bob 两人轮流建造灯塔，Alice 先手。 每一次操作只能选择一个空地建造灯塔，并且要保证这个位置不能被先前建造的任意一个灯塔侦测到。 如果某人无法操作了，那么 ta 就输了。 假设两个人都绝对聪明，问最终胜者是谁？

仅一行，包含三个整数 $n,m,k\ (1\le n,m,k\le 10^9)$。

如果先手必胜，在一行内输出 `Alice`，否则输出 `Bob`。

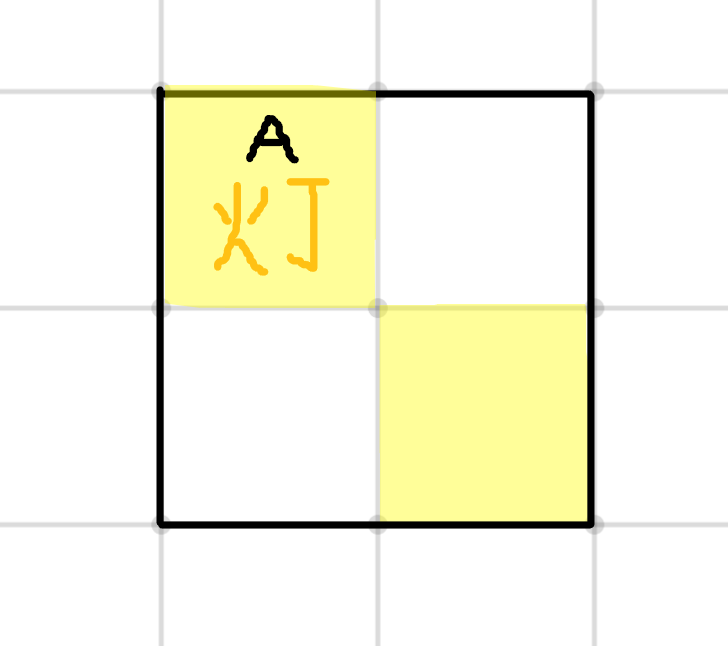
不管 Alice 第一轮放在哪里，都会变成类似以下这种局面：  然后 Bob 随意一放，Alice 就没有地方放了，Bob 胜利。