【Tutorial】Round 1 (Div. 2)

# A - 交换尾巴都是正整数，没有什么需要注意的，实现即可。时间复杂度 $O(1)$ <details> <summary>代码 - 字符串</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int main() {     string a, b;     cin >> a >> b;     swap(a.back(), b.back());     cout << a << " " << b;     return 0; } </code></pre> </details> <details> <summary>代码 - 整数</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int main() {     int a, b;     cin >> a >> b;     cout << a / 10 * 10 + b % 10 << " " << b / 10 * 10 + a % 10;     return 0; } </code></pre> </details> --- # B - 分割序列要想分成三段连续子序列且和相同，首先和必须是 $3$ 的倍数。然后发现第一段和第三段最好处理，一定是原序列的前缀和后缀。因此求出总和并除以 $3$ 后作为目标总和，找原序列的前后缀各自需要多长才能使其和等于目标总和。贪心，记 $prex$ 表示满足 $\sum\limits_{i=1}^{prex} a_i = \dfrac{sum}{3}$ 的**最小**下标，而 $sufx$ 表示满足 $\sum\limits_{i=sufx}^{n} a_i = \dfrac{sum}{3}$ 的**最大**下标。明显在理想情况下，序列可以分为 $[1, prex], [prex+1, sufx-1], [sufx, n]$ 这样总和相同的三段。如果找不到满足条件的 $prex$ 或 $sufx$，则答案不存在。但需要额外考虑最后一种情况，即中间这一段区间 $[prex + 1, sufx - 1]$ 是否存在。举例：`1 -1 -1 1` 这四个数总和为 $0$，按照上述方法找到的 $prex = 2, sufx = 3$，明显不符合题意中“非空连续子序列”的描述。时间复杂度 $O(\sum n)$ <details> <summary>代码</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; typedef long long ll; int a[100005]; int main() {     int T;     cin >> T;     while(T--)     {         int n;         cin >> n;         ll sum = 0;         for(int i = 1; i <= n; i++)         {             cin >> a[i];             sum += a[i];         }         if(sum % 3 != 0)         {             cout << "NO\n";             continue;         }         sum /= 3;                  int prex = 0, sufx = 0; // prex 记录前缀到哪个下标过才能让总和 = sum，sufx 则记录后缀                  ll tmp = 0;         for(int i = 1; i <= n; i++)         {             tmp += a[i];             if(tmp == sum)             {                 prex = i;                 break;             }         }                  tmp = 0;         for(int i = n; i >= 1; i--)         {             tmp += a[i];             if(tmp == sum)             {                 sufx = i;                 break;             }         }                  if(prex != 0 && sufx != 0 && sufx - prex >= 2)             cout << "YES\n";         else             cout << "NO\n";     }     return 0; } </code></pre> </details> --- # C - 同余式如果 $a, b$ 两非负整数满足： $$ a \equiv b \pmod m $$ 记它们除以 $m$ 的余数为 $t$，则 $a$ 和 $b$ 可以描述成： $$ a = k_1m + t \quad (k_1 \in \N)\\ b = k_2m + t \quad (k_2 \in \N) $$ 则： $$ a - b = (k_1 - k_2)m $$ 发现两数的差值一定是 $m$ 的倍数，换言之，$m$ 一定是两数差值的因数。找出 $\ge 2$ 的最小的 $|a-b|$ 的因数即可。记得加上根号优化，防止 $|a-b|$ 是一个大质数的情况。特殊讨论： - $|a-b| = 0$，任何正整数都可以看作 $0$ 的因数，答案即 $2$； - $|a-b|=1$，只有 $1$ 是 $1$ 的因数，因此答案不存在，输出 $-1$。时间复杂度 $O(\sqrt{|a-b|})$ <details> <summary>代码 - 根号优化找因数</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int main() {     int a, b;     cin >> a >> b;     int c = abs(a - b);     if(c == 0)         cout << "2";     else if(c == 1)         cout << "-1";     else     {         int d = sqrt(c);         for(int i = 2; i <= d; i++)         {             if(c % i == 0)             {                 cout << i;                 return 0;             }         }         cout << c;     }     return 0; } </code></pre> </details> --- # D - 勇闯地下城我们记 $X$ 为最终答案，即能够击败所有 BOSS 的前提下的初始最小武力值。发现，只要我们的初始武力值 $\ge X$，一定都能够击败所有 BOSS；而只要初始武力值 $\lt X$，肯定就无法击败所有 BOSS 了。答案明显满足二分性质，考虑如何检查答案是否满足条件即可。 `check` 函数中，既然知道了初始武力值是多少，剩下的就可以直接模拟了，统计过程中有多少只 BOSS 没法直接打过，最终与 $m$ 判断下大小即可。时间复杂度 $O(n\log X), X_{max} = 10^9$ <details> <summary>代码 - 二分</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int n, m, a[200005], b[200005]; bool check(long long v) {     int t = m; // 剩余的全员参战次数     for(int i = 1; i <= n; i++)     {         if(v >= a[i]) // 能打过就直接打，并吸收能力值             v += b[i];         else             t--;     }     return t >= 0; // 使用全员参战的次数只要不超过 m 就说明当前初始武力值有效 } int main() {     scanf("%d%d", &n, &m);     for(int i = 1; i <= n; i++)         scanf("%d%d", &a[i], &b[i]);          int l = 1, r = 1e9;     while(l <= r)     {         int mid = l + r >> 1;         if(check(mid))             r = mid - 1;         else             l = mid + 1;     }          printf("%d\n", l);          return 0; } </code></pre> </details> --- # E - 小新的01矩阵对于行来说，如果我们把前面的行上的 $1$ 全部翻成 $0$ 了，而后面的行上还有 $1$ 的话，肯定还是要翻后面行上的 $1$ 的。但根据题意，翻后面的行一定又会对前面的行产生影响。所以不如先翻后面的行上的 $1$，再翻前面的行上的 $1$ 最优。对于列来说，同上。因此，我们可以通过循环嵌套，从最后一行最后一列的位置开始，同一列从后往前，然后按行从下往上一个个处理即可，每发现当前数字为 $1$，就以当前位置作为右下角，把整个左上矩阵全部翻一次。 <details> <summary>代码 - 暴力</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int n, a[2005][2005]; int main() {     cin >> n;     for(int i = 1; i <= n; i++)         for(int j = 1; j <= n; j++)         {             char c;             cin >> c;             a[i][j] = c - '0';         }          int ans = 0;     for(int i = n; i >= 1; i--)         for(int j = n; j >= 1; j--)         {             if(a[i][j] == 1)             {                 ans++;                 // 以 (i, j) 作为右下角，对左上角子矩阵进行翻转                 for(int x = 1; x <= i; x++)                     for(int y = 1; y <= j; y++)                         a[x][y] = 1 - a[x][y]; // 01 翻转             }         }     cout << ans;          return 0; } </code></pre> </details> 但很明显，这是 $O(N^4)$ 的时间复杂度，无法通过本题。考虑每次翻转，都需要把以当前点作为右下角的整个左上方都 0/1 翻转一次，是否可以采用什么方法，快速把翻转完成？二维线段树或者二维树状数组，想写的话也可以写。但，换位思考一下，我们如果在处理每个数字时，能够求出在此之前它已经被翻转了几次了的话，那就不用每次模拟翻转了。明显，如果当前位置被翻转了，那么翻转的来源（或者说之前选择了哪个位置作为右下角翻转的）一定是在当前位置的右下角的子矩阵内。根据我们的枚举顺序，我们本就是倒着处理矩阵中每个数字的，因此可以做一个二维后缀和，在枚举的同时推出当前位置被翻转了多少次即可。最后如果满足“当前数字为 $1$，被翻了偶数次”或者“当前数字为 $0$，被翻了奇数次”的话，说明我们需要以当前位置作为右下角，翻一次整个左上角的子矩阵，那么就在二位后缀和数组中标记一下即可。时间复杂度 $O(N^2)$ <details> <summary>代码 - 二维后缀和</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; int n, a[2005][2005], b[2005][2005]; int main() {     cin >> n;     for(int i = 1; i <= n; i++)         for(int j = 1; j <= n; j++)         {             char c;             cin >> c;             a[i][j] = c - '0';         }          int ans = 0;     for(int i = n; i >= 1; i--)         for(int j = n; j >= 1; j--)         {             b[i][j] = b[i+1][j] + b[i][j+1] - b[i+1][j+1];             if((a[i][j] + b[i][j]) & 1)             {                 ans++;                 b[i][j]++;             }         }     cout << ans;          return 0; } </code></pre> </details> --- # F - 多多的纸片排列先说结论：所有半径为 $2$ 的纸片放中间，然后把半径为 $1$ 的纸片放两侧是最优秀的排列。换句话说，**尽可能不要让半径为 $2$ 的纸片出现在两侧，并且尽可能不要让不同类型的纸片交替出现**。 ~~至于结论的由来，请自行打表。（×）~~ 那么圆心移动总距离如何计算？我们把小圆的运动轨迹分成 $n+m+1$ 段，即：从最左侧底部滚到第 $1$ 个圆的正上方（圆心对齐），然后从第 $1$ 个圆的正上方滚到第 $2$ 个圆的正上方，如此继续往下，直到滚到最后一个圆的正上方，最后滚到最右侧底部结束。接下来先分几种情况讨论长度。解法有很多种，这里每种情况只讲一种。记小圆从最左（最右）侧底部滚到半径为 $1$ 的圆正上方所经过的距离为 $a_1$，$a_1 = $ 半径为 $2$ 且弧度为 $\dfrac \pi 2$ $(90^{\circ})$ 的圆弧长 $ = \dfrac \pi 2 \times 2 = \pi$. 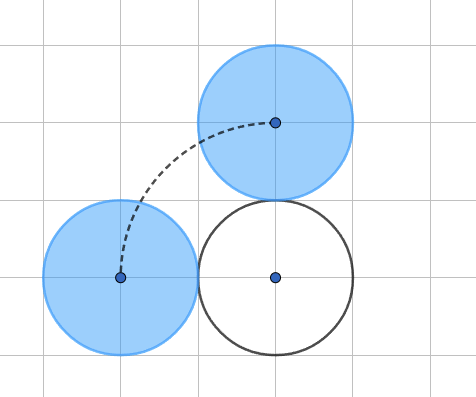![1718651835546.png](/userfiles/blog-images/e6be6c50-e23b-4b56-85d3-aff30645caa1.png) 记小圆从最左（最右）侧底部滚到半径为 $2$ 的圆正上方所经过的距离为 $a_2$，$a_2 = $ 半径为 $3$ 且弧度为 $\dfrac \pi 2 + \theta$ 的圆弧长 $ = (\dfrac \pi 2 + \theta) \times 3$。其中我们从底部小圆作垂线到与半径为 $2$ 的圆同高的位置，可以得知 $\sin\theta = \dfrac 1 3$，因此 $\theta = \arcsin\dfrac 1 3$，即 $a_2 = (\dfrac \pi 2 + \arcsin\dfrac 1 3) \times 3$. 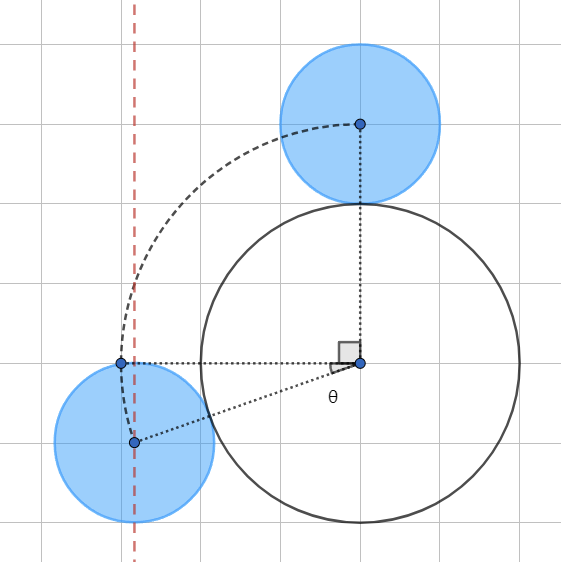![1718651840641.png](/userfiles/blog-images/239489cb-f386-42c6-b62f-2977eee024d1.png) 记小圆从半径为 $1$ 的圆顶部移动到半径为 $1$ 的圆顶部所经过的距离为 $b_{11}$。如果能直接发现三圆相切时圆心组成等边三角形的话，可以直接得出 $\alpha = 60^{\circ}, \beta = 30^{\circ}$。而如果不能，我们从小圆移动到与两圆刚好相切时的中点向下作一条垂线。已知 $\alpha + \beta = 90^{\circ}$，且 $\cos\alpha = \dfrac 1 2$，因此 $\alpha = \arccos\dfrac 1 2 = 60^{\circ}$，$\beta = 90^{\circ} - \alpha = 30^{\circ}$。那么 $b_{11} = $ 两段半径为 $2$ 且弧度为 $\dfrac \pi 6$ $(30^{\circ})$ 的圆弧长 $= 2 \times \dfrac \pi 6 \times 2 = \dfrac {3\pi} 2$. 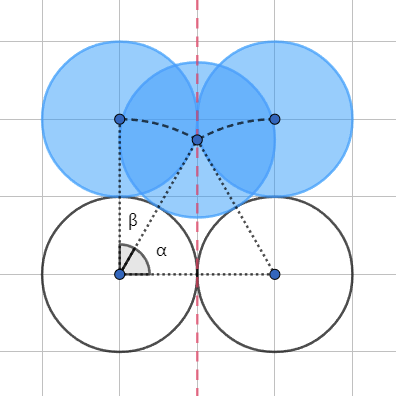![1718651846499.png](/userfiles/blog-images/6bf3e168-e024-4a6d-9632-40c213be474f.png) 记小圆从半径为 $2$ 的圆顶部移动到半径为 $2$ 的圆顶部所经过的距离为 $b_{22}$。同上，我们从小圆移动到与两圆刚好相切时的中点向下作一条垂线。已知 $\alpha + \beta = 90^{\circ}, \alpha + \gamma = 90^{\circ}$，因此 $\beta = \gamma$。$\sin \beta = \sin \gamma = \dfrac 2 3$，因此 $\beta = \arcsin\dfrac 2 3$。那么 $b_{22} = $ 两段半径为 $3$ 且弧度为 $\arcsin \dfrac 2 3$ 的圆弧长 $= 2 \times \arcsin \dfrac 2 3 \times 3 = 6 \arcsin \dfrac 2 3$. 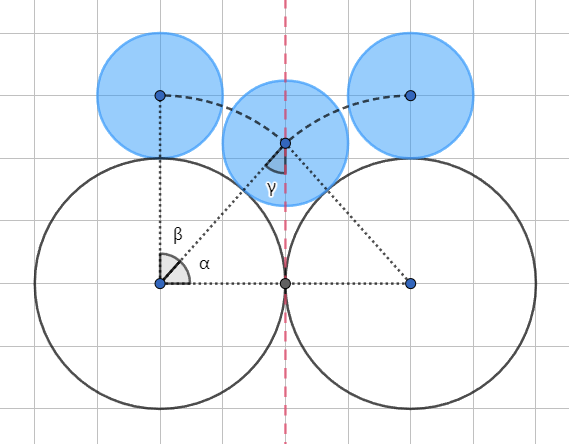![1718651851171.png](/userfiles/blog-images/8ac93113-37ca-4a17-b7ac-a5278faebf1c.png) 记小圆从半径为 $2$ 的圆顶部移动到半径为 $1$ 的圆顶部所经过的距离为 $b_{21}$，从半径为 $1$ 的圆顶部移动到半径为 $2$ 的圆顶部所经过的距离为 $b_{12}$，发现 $b_{21} = b_{12}$。明显发现小圆与半径为 $1$ 的圆的切点和半径为 $2$ 的圆的圆心在同一水平线上，且小圆的圆心与半径为 $1$ 的圆的圆心在同一条竖直线上，两线相互垂直。即 $\alpha + \beta = 90^{\circ}$，$\sin \alpha = \dfrac 1 3$，即 $\alpha = \arcsin \dfrac 1 3$，那么 $\beta = 90^{\circ} - \arcsin \dfrac 1 3$。那么 $b_{21} = $ 半径为 $3$ 且弧度为 $\dfrac \pi 2 - \arcsin \dfrac 1 3$ 的圆弧长 $= (\dfrac \pi 2 - \arcsin \dfrac 1 3) \times 3$. 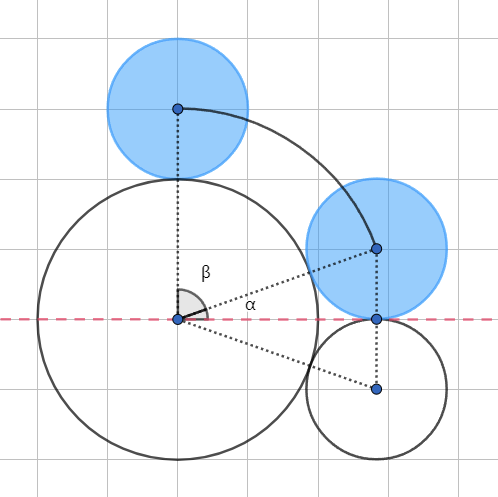![1718651855438.png](/userfiles/blog-images/d87c6ea9-d535-4f95-a18a-5770e8b5a710.png) 综上，各种情况下对应的答案均已求出。考虑本题，根据半径为 $1$ 的纸片数量 $n$ 和半径为 $2$ 的纸片数量 $m$ 进行分类讨论： - 如果 $m = 0$，那么小圆会从底部滚到第一个半径为 $1$ 的纸片上，中间经过 $n - 1$ 段 $b_{11}$，再从最后一个半径为 $1$ 的纸片上滚到底部，总答案为 $a_1 + (n-1)b_{11} + a_1$. - 如果 $m \ne 0$： - 如果 $n = 0$，那么小圆会从底部滚到第一个半径为 $2$ 的纸片上，中间经过 $m - 1$ 段 $b_{22}$，再从最后一个半径为 $2$ 的纸片上滚到底部，总答案为 $a_2 + (m-1)b_{22} + a_2$. - 如果 $n = 1$，此时只有一个半径为 $1$ 的纸片，可以放在最前面也可以放在最后面。假设放在最前面，那么小圆会从底部滚到第一个半径为 $1$ 的纸片上，然后再从半径为 $1$ 的纸片上滚到半径为 $2$ 的纸片上，中间经过 $m - 1$ 段 $b_{22}$，再从最后一个半径为 $2$ 的纸片上滚到底部，总答案为 $a_1 + b_{12} + (m - 1)b_{22} + a_2$. - 如果 $n \ge 2$，那么序列两边必须都有半径为 $1$ 的纸片，且半径为 $2$ 的纸片在中间连续出现。假设最前面有一张半径为 $1$ 的纸片，然后放 $m$ 张半径为 $2$ 的纸片，最后把剩下的 $n-1$ 张半径为 $1$ 的纸片都放完，那么小圆会从底部滚到第一个半径为 $1$ 的纸片上，然后再从半径为 $1$ 的纸片上滚到半径为 $2$ 的纸片上，中间经过 $m - 1$ 段 $b_{22}$，然后再从半径为 $2$ 的纸片上滚到半径为 $1$ 的纸片上，中间再经过 $n-2$ 段 $b_{11}$，再从最后一个半径为 $1$ 的纸片上滚到底部，总答案为 $a_1 + b_{12} + (m-1)b_{22} + b_{21} + (n-2)b_{11} + a_1$. 时间复杂度 $O(1)$ <details> <summary>代码</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; const double PI = acos(-1); const double a1 = PI; const double a2 = 1.5 * PI + 3 * asin(1.0 / 3); const double b11 = 2.0 / 3 * PI; const double b12 = 1.5 * PI - 3 * asin(1.0 / 3); const double b21 = b12; const double b22 = 6 * asin(2.0 / 3); int main() {     int x, y;     scanf("%d%d", &x, &y);          if(y == 0)         printf("%.3f", a1 + (x - 1) * b11 + a1);     else     {         if(x == 0)             printf("%.3f", a2 + (y - 1) * b22 + a2);         else if(x == 1)             printf("%.3f", a1 + b12 + (y - 1) * b22 + a2);         else             printf("%.3f", a1 + b12 + (y - 1) * b22 + b21 + (x - 2) * b11 + a1);     }     return 0; } </code></pre> </details> --- # G - 看来是一个麻烦的序列捏如果求的只是所有**非空连续子序列**的和，那么本题会是一道比较简单的问题，单独考虑每个位置上的数字 $a_i$，统计其对答案的贡献即可。非空连续子序列可以看作是原序列的一段区间，也就是说 $a_i$ 对答案的贡献 $=$ 有多少种不同的区间包含 $i$ 乘上 $a_i$ 所得到的数字。左端点 $l \le i$，右端点 $r \ge i$ 的情况数为 $i \times (n - i + 1)$，因此答案为 $\sum\limits_{i = 1}^n i \times (n - i + 1) \times a_i$. 如果求的只是所有**非空子序列**的和，那么更简单，每个数字在每种子序列中只有出现和不出现两种情况。由于长度为 $n$ 的序列的子序列共有 $2^n$ 种（包含空子序列也没关系反正答案 $=0$），那么每个数字出现的次数明显就是 $2^{n-1}$ 次，答案为 $\sum\limits_{i=1}^n 2^{n-1}\times a_i$. 但本题把两种情况嵌套起来了。没关系，按照上面的方法类似地进行思考，我们还是单独考虑每个 $a_i$ 对于答案的贡献。对于 $a_i$，我们根据其左右两侧分别还需要再选多少个数字和他一起组成一个非空子序列进行考虑。记左侧有 $x$ 个数（$0 \le x \le i-1$），右侧有 $y$ 个数（$0 \le y \le n - i$），满足这种条件的非空子序列共有 $C_{i-1}^x \times C_{n-i}^y$ 种。在每一种非空子序列的连续非空子序列中， $a_i$ 都会出现 $(x+1) \times (y+1)$ 次。因此我们如果能够枚举每种 $x, y$，答案很明显就等于： $$ \sum_{i=1}^n\sum_{x=0}^{i-1}\sum_{y=0}^{n-i}C_{i-1}^xC_{n-i}^y(x+1)(y+1)a_i $$ <details> <summary>代码 - 暴力</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod = 1000000007; int n; ll a[200005]; ll fac[200005], inv[200005]; ll qpow(ll a, ll n) {     ll r = 1;     while(n)     {         if(n & 1)             r = r * a % mod;         a = a * a % mod;         n >>= 1;     }     return r; } ll getC(int n, int m) {     return fac[n] * inv[m] % mod * inv[n - m] % mod; } int main() {     cin >> n;     for(int i = 1; i <= n; i++)         cin >> a[i];          fac[0] = 1;     for(int i = 1; i <= n; i++)         fac[i] = fac[i - 1] * i % mod;     inv[n] = qpow(fac[n], mod - 2);     for(int i = n - 1; i >= 0; i--)         inv[i] = inv[i + 1] * (i + 1) % mod;          ll ans = 0;     for(int i = 1; i <= n; i++)     {         for(int x = 0; x <= i - 1; x++)         {             for(int y = 0; y <= n - i; y++)             {                 ll tmp = getC(i - 1, x) * getC(n - i, y) % mod * (x + 1) % mod * (y + 1) % mod * a[i] % mod;                 ans = (ans + tmp) % mod;             }         }     }     cout << ans;          return 0; } </code></pre> </details> 但这种做法的时间复杂度是 $O(n^3)$ 的，显然不可行，进一步尝试化简式子： $$ \left . \begin{aligned} &\sum_{i=1}^n\sum_{x=0}^{i-1}\sum_{y=0}^{n-i}C_{i-1}^xC_{n-i}^y(x+1)(y+1)a_i\\ =&\sum_{i=1}^na_i\cdot \sum_{x=0}^{i-1}\sum_{y=0}^{n-i}C_{i-1}^xC_{n-i}^y(x+1)(y+1)\\ =&\sum_{i=1}^na_i\cdot \sum_{x=0}^{i-1}C_{i-1}^x(x+1)\cdot \sum_{y=0}^{n-i}C_{n-i}^y(y+1) \end{aligned} \right . $$ 记 $f_i = \sum\limits_{x=0}^{i}C_i^x(x+1)$，那么上式可化成： $$ \sum_{i=1}^na_i\cdot f_{i-1}\cdot f_{n-i} $$ 于是我们考虑预处理 $f_i$，得到以下代码： <details> <summary>代码 - 优化</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod = 1000000007; int n; ll a[200005], f[200005]; ll fac[200005], inv[200005]; ll qpow(ll a, ll n) {     ll r = 1;     while(n)     {         if(n & 1)             r = r * a % mod;         a = a * a % mod;         n >>= 1;     }     return r; } ll getC(int n, int m) {     return fac[n] * inv[m] % mod * inv[n - m] % mod; } int main() {     cin >> n;     for(int i = 1; i <= n; i++)         cin >> a[i];          fac[0] = 1;     for(int i = 1; i <= n; i++)         fac[i] = fac[i - 1] * i % mod;     inv[n] = qpow(fac[n], mod - 2);     for(int i = n - 1; i >= 0; i--)         inv[i] = inv[i + 1] * (i + 1) % mod;          for(int i = 0; i <= n; i++)         for(int x = 0; x <= i; x++)             f[i] = (f[i] + getC(i, x) * (x + 1) % mod) % mod;          ll ans = 0;     for(int i = 1; i <= n; i++)         ans = (ans + a[i] * f[i - 1] % mod * f[n - i] % mod) % mod;     cout << ans;          return 0; } </code></pre> </details> 但明显预处理的过程还是 $O(n^2)$ 的，所以考虑进一步优化预处理的过程： $$ \left . \begin{aligned} f_i &= \sum\limits_{x=0}^{i}C_i^x(x+1)\\ &= 1C_i^0 + 2C_i^1 + 3C_i^2 + \dots + (i+1)C_i^i \quad (1) \end{aligned} \right . $$ 根据组合数 $C_n^m = C_n^{n-m}$，得： $$ f_i = 1C_i^i + 2C_i^{i-1} + 3C_i^{i-2} + \dots + (i+1)C_i^0 \quad (2) $$ 合并上面 $(1), (2)$ 两式： $$ \left . \begin{aligned} f_i + f_i &= (i+2)C_i^0 + (i+2)C_i^1 + (i+2)C_i^2 \dots + (i+2)C_i^i\\ 2f_i &= (i+2) (C_i^0 + C_i^1 + C_i^2 + \dots + C_i^i) \end{aligned} \right . $$ 根据二项式系数和的性质可知 $C_n^0 + C_n^1 + C_n^2 + \dots + C_n^n = 2^n$，得： $$ \left . \begin{aligned} 2f_i &= (i+2)2^i\\ f_i &= (i+2)2^{i-1} \end{aligned} \right . $$ 于是可以通过预处理 $2$ 的幂次，或是直接套快速幂来解决该题。时间复杂度 $O(n)$ 或 $O(n\log n)$ （快速幂） <details> <summary>代码 - 最终</summary> <pre><code class='cpp language-cpp'> #include<bits/stdc++.h> using namespace std; typedef long long ll; const ll mod = 1000000007; int n; ll a[200005], f[200005]; ll p2[200005]; int main() {     cin >> n;     for(int i = 1; i <= n; i++)         cin >> a[i];          p2[0] = 1;     for(int i = 1; i <= n; i++)         p2[i] = p2[i - 1] * 2 % mod;          f[0] = 1;     for(int i = 1; i <= n; i++)         f[i] = (i + 2) * p2[i - 1] % mod;          ll ans = 0;     for(int i = 1; i <= n; i++)         ans = (ans + a[i] * f[i - 1] % mod * f[n - i] % mod) % mod;     cout << ans;          return 0; } </code></pre> </details>

评论列表

登录